quarta-feira, 21 de janeiro de 2009

Matemática

Teorema de Pitágoras

O Teorema de Pitágoras é provavelmente o mais célebre dos teoremas da matemática. Enunciado pela primeira vez por filósofos gregos chamados de pitagóricos, estabelece uma relação simples entre o comprimento dos lados de um triângulo retângulo:

O quadrado da hipotenusa é igual à soma dos quadrados dos catetos .

Se c designar o comprimento da hipotenusa e a e b os comprimentos dos catetos, o teorema afirma que:

c^2 = a^2 + b^2.\,
Aplicações do teorema

O teorema de Pitágoras pode ser aplicado em diversas figuras:

Quadrado

A diagonal do quadrado divide-o em dois triângulos retângulos congruentes. Sendo l o lado e d a diagonal, podemos definir que:

l^2+l^2=d^2\,\! \Rightarrow

2l^2=d^2\,\! \Rightarrow d=\sqrt{2l^2}\,\! \Rightarrow d= l \sqrt{2}\,\!.

Triângulo equilátero

A altura do triângulo equilátero divide-o em dois triângulos retângulos congruentes; sendo l o lado e h a altura, podemos definir que:

l^2=\left(\frac{l}{2}\right)^2+h^2\,\! \Rightarrow l^2=\frac{l^2}{4}+h^2\,\! \Rightarrow \frac{4l^2}{4}= \frac{l^2}{4} + \frac{4h^2}{4}\,\! \Rightarrow 4l^2=l^2+4h^2\,\! \Rightarrow 4h^2=3l^2\,\! \Rightarrow h^2=\frac{3l^2}{4}\,\! \Rightarrow h= \sqrt{\frac{3l^2}{4}}\,\! \Rightarrow h = \frac{l\sqrt3}{2}\,\!.

Generalizações


O teorema de Pitágoras permite calcular um lado de um triângulo rectângulo conhecendo os outros dois. O teorema dos cossenos permite calculá-lo num triângulos qualquer.

O teorema de Pitágoras pode ser generalizado para um n- simlex rectângulo: o quadrado do (n-1)-volume da hipotenusa é igual à soma dos quadrados dos (n-1)-volumes dos catetos. Em particular, num tetraedro rectângulo (isto é, que tem 3 faces perpendicular entre si - os catetos), o quadrado da área da hipotenusa (a face que não é perpendicular às restantes) é igual à soma dos quadrados das áreas dos catetos.

Pitágoras dizia que"em todo triângulo retângulo, a soma das áreas dois quadrados dos catetos é igual à área dos quadrados da hipotenusa".

O teorema de Pitágoras na geometria esférica e hiperbólica

Seja c a hipotenusa de um triângulo rectângulo numa geometria não euclidiana e a e b os catetos. O Teorema de Pitágoras toma uma das seguintes formas:

na geometria esférica, tem-se

\cos(c)=\cos(a)\cos(b)\,\!

na geometria hiperbólica tem-se

\cosh(c)=\cosh(a)\cosh(b)\,\!


Curva de Gauss

A distribuição normal é uma das mais importantes distribuições da estatística, conhecida também como Distribuição de Gauss ou Gaussiana. Foi desenvolvida pelo matemático francês Abraham de Moivre.

Além de descrever uma série de fenômenos físicos e financeiros, possui grande uso na estatística inferencial. É inteiramente descrita por seus parâmetros de média e desvio padrão, ou seja, conhecendo-se estes consegue-se determinar qualquer probalidade em uma Normal.

Um interessante uso da Distribuição Normal é que ela serve de aproximação para o cálculo de outras distribuições quando o número de observações fica grande. Essa importante propriedade provem do teorema central do limite que diz que "toda soma de variáveis aleatórias independentes de média finita e variância limitada é aproximadamente Normal, desde que o número de termos da soma seja suficientemente grande" (ver o teorema para um enunciado mais preciso).

Função de densidade de probabilidade

A fução desidade de probabilidade da distribuição normal com média μ e variância σ2 (de forma equivalente, desvio padrão σ) é assim definida,

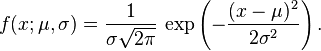
f(x;\mu,\sigma) = \frac{1}{\sigma\sqrt{2\pi}} \, \exp \left( -\frac{(x- \mu)^2}{2\sigma^2} \right).

Se a variável aleatória X segue esta distribuição escreve-se: X ~ N(μ,σ2). Se μ = 0 e σ = 1, a distribuição é chamada de distribuição normal padrão e a função de densidade de probabilidade reduz-se a,

f(x) = \frac{1}{\sqrt{2\pi}} \, \exp\left(-\frac{x^2}{2} \right).
Propriedades

  • Se X segue uma distribuição normal, então a X + b também segue.
  • Se X e Y são distribuições normais independentes, então sua soma U = X + Y, sua diferença V = X - Y ou qualquer combinação linear W = a X + b Y também são distribuições normais.
    • É fácil construir exemplos de distribuições normais X e Y dependentes (mesmo com correlação zero) cuja soma X + Y não é normal. Por exemplo, seja X uma distribuição normal padrão (média 0 e variância 1), então fixando-se um número real positivo a, seja Ya definida como X sempre que |X| <>a também é uma normal e X + Ya é uma variável aleatória que nunca pode assumir valores de módulo acima de 2 a (ou seja, não é normal). Quando a é muito pequeno, X e Y são praticamente opostas, e sua correlação é próxima de -1. Quando a é muito grande, X e Y são praticamente idênticas, e sua correlação é próxima de 1. Como a correlação entre X e Ya varia continuamente com a, existe um valor de a para o qual a correlação é zero.
  • A soma de uma grande quantidade de variáveis aleatórias (com algumas restrições) tende a uma distribuição normal - o significado mais preciso disto é o teorema do limite central.
  • A distribuição normal é infinitamente divisível, no seguinte sentido: se X é uma variável aleatória que segue uma distribuição normal e n é um número natural, então existem n variáveis aletórias X_1, X_2, \ldots X_n\,, independentes e indenticamente distribuídas, tal que
X = X_1 + X_2 + \ldots + X_n\,
Distribuições relacionadas

  • R˜Rayleigh(σ2) é a distribuição de Rayleigh se 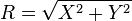R = \sqrt{X^2 + Y^2} onde X˜N(0,σ2) e Y˜N(0,σ2) são duas distribuições normais independentes.
  • Y \sim \chi_{\nu}^2 é a distribuição Chi-quadrado com ν graus de liberdade se Y = \sum_{k=1}^{\nu} X_k^2 em que Xk˜N(0,1) para k=0,1,\cdots,\nu são distribuições normais padrão independentes.
  • Y˜Cauchy(μ = 0,θ = 1) é a distribuição de Cauchy se Y = X1 / X2 para X1˜N(0,1) e X2˜N(0,1) são duas distribuições normais padrão independentes.
  • Y˜Log-N(μ,σ2) é a disribuião log-normal se Y = eX e X˜N(μ,σ2).
  • Relação com Lévy skew alpha-stable distribution: se 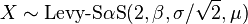X\sim \textrm{Levy-S}\alpha\textrm{S}(2,\beta,\sigma/\sqrt{2},\mu) então X˜N(μ,σ2).
  • Distribuição normal truncada: Se X˜N(μ,σ2) então, truncando para valores entre A e B temos uma variável aleatória contínua com média E(X)=\mu + \frac{\sigma(\phi_1-\phi_2)}{T}, em que T=\Phi\left(\frac{B-\mu}{\sigma}\right)-\Phi\left(\frac{A-\mu}{\sigma}\right), \phi_1=f\left(\frac{A-\mu}{\sigma}\right) e \phi_2=f\left(\frac{B-\mu}{\sigma}\right), sendo f(\cdot) a função desidade de probabilidade e \Phi(\cdot) a fução de probabilidade acumulada de uma distribuição normal padrão.

Postado por às

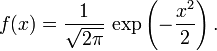
Nenhum comentário:

Postar um comentário

Assinar: Postar comentários (Atom)